EψωMom = energia, ondas, fótons, frequência, momentum. EM :

 / E =EψωMom   [/ ] /  

 / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 é a massa da partícula.

 é a carga da partícula.

 é um vetor de três componentes do dois-por-dois das matrizes de Pauli. Isto significa que cada componente do vetor é uma matriz de Pauli.

 é o vetor de três componentes da dinâmica dos operadores. Os componentes desses vetores são: 

 é o vetor de três componentes do potencial magnético.

 é o potencial escalar elétrico.

 são os dois componentes spinor da onda, podem ser representados como .

 

G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ].

EψωMom = energia, ondas, fótons, frequência, momentum.

EQUAÇÃO GENERALIZADA DE GRACELI.

Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

 equação de Graceli.

1 /   [r  t ].  ψ   - G ψ  = E ψ  [r  t ]. / [ - 1 ]. [-1]

Equação de Born-Landé-Graceli.

1/  E =   [/ ] /        [-1/ ]  [-1]       (Joules/mol)

 = número de Avogadro

 = constante de Madelung, relacionada com a geometria do cristal.

 = carga do cátions em unidade eletrostática

 = carga do ânion em unidade eletrostática

 = carga elementar, 1,6022×10−19 C

 = permissividade,  = 8,8541878176×10−12 F m

 = distância do íon mais próximo em metros

 = expoente de Born, um número entre 5 e 12, determinado experimentalmente pela medida de compressibilidade do sólido ou derivado teoricamente.[3]

 é a massa da partícula.

 é a carga da partícula.

 é um vetor de três componentes do dois-por-dois das matrizes de Pauli. Isto significa que cada componente do vetor é uma matriz de Pauli.

 é o vetor de três componentes da dinâmica dos operadores. Os componentes desses vetores são: 

 é o vetor de três componentes do potencial magnético.

 é o potencial escalar elétrico.

 são os dois componentes spinor da onda, podem ser representados como .

 

G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ].

EψωMom = energia, ondas, fótons, frequência, momentum.

EQUAÇÃO GENERALIZADA DE GRACELI.

Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

1 / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..[1-].

 equação de Graceli.

  [r  t ].  ψ   - G ψ  = E ψ  [r  t ]. / [ - 1 ].

Equação Graceli.

 E =EψωMom   [/ ] /        [-1/ ]         (Joules/mol)

 = número de Avogadro

 = constante de Madelung, relacionada com a geometria do cristal.

 = carga do cátions em unidade eletrostática

 = carga do ânion em unidade eletrostática

 = carga elementar, 1,6022×10−19 C

 = permissividade,  = 8,8541878176×10−12 F m

 = distância do íon mais próximo em metros

 = expoente de Born, um número entre 5 e 12, determinado experimentalmente pela medida de compressibilidade do sólido ou derivado teoricamente.[3]

 Como as partículas são indistinguíveis na estatística de Fermi-Dirac, a especificação do número de partículas é suficiente para determinarmos o estado do gás. Como os férmions obedecem ao princípio de exclusão de Pauli, não é possível que mais de uma partícula esteja no mesmo estado, se faz apenas necessário somar sobre todos os números possíveis de partículas em um único estado, ou seja, os dois possíveis valores ^[5]:

${\displaystyle n_{r}=0,1}$ para cada ${\displaystyle r}$

Quando o número total de partículas ${\displaystyle N}$ é fixado, a soma sobre todos os valores possíveis de ${\displaystyle n_{r}}$, com ${\displaystyle n_{1},n_{2},...}$ segue a seguinte relação

${\displaystyle \sum _{r}n_{r}=N}$ / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Dado um sistema com ${\displaystyle N}$ férmions em equilíbrio térmico a uma temperatura arbitrária ${\displaystyle T}$, o número médio de partículas ${\displaystyle <n_{s}>}$ em um estado particular ${\displaystyle s}$ com energia ${\displaystyle \epsilon _{s}}$ é obtido através da distribuição canônica, logo^[5]

${\displaystyle <n_{s}>={\frac {\sum _{n_{s}}n_{s}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}{\sum _{n_{s}}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

no qual ${\displaystyle \beta ={\frac {1}{k_{B}T}}}$, / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..sendo  a constante de Boltzmann. Podemos renomear alguns termos na expressão acima, de forma que obtemos

${\displaystyle Z_{s}(N)=\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Somando sobre ${\displaystyle n_{s}}$ = 0 e 1, temos

${\displaystyle <n_{s}>={\frac {e^{-\beta \epsilon _{s}}Z_{s}(N-1)}{Z_{s}(N)+e^{-\beta \epsilon _{s}}Z_{s}(N-1)}}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

ou, ainda, podemos simplificar:

${\displaystyle <n_{s}>={\frac {1}{[Z_{s}(N)/Z_{s}(N-1)]e^{\beta \epsilon _{s}}+1}}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Na condição em que ${\displaystyle \Delta N\ll N}$, podemos escrever

${\displaystyle lnZ_{s}(N-\Delta N)=lnZ_{s}(N)-{\frac {\partial lnZ_{s}}{\partial N}}\Delta N=lnZ_{s}(N)-\alpha _{s}\Delta N}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

${\displaystyle Z_{s}(N-\Delta N)=Z_{s}(N)e^{-\alpha _{s}\Delta N}}$ 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

com ${\displaystyle \alpha _{s}={\frac {\partial lnZ_{s}}{\partial N}}}$. Como ${\displaystyle Z_{s}(N)}$ é uma soma sobre muitos estados, a variação de seu logaritmo com o número de partículas total ${\displaystyle N}$ não é afetado por qual estado particular ${\displaystyle s}$ foi omitido no somatório. Portanto, podemos fazer uma aproximação em que ${\displaystyle \alpha _{s}}$ é independente de ${\displaystyle s}$:

${\displaystyle \alpha _{s}=\alpha }$

Ainda, podemos aproximar ${\displaystyle \alpha }$ em termos da derivada da função partição ${\displaystyle \mathrm {Z} (N)}$ sobre todos os estados, assim^[5]:

${\displaystyle \alpha ={\frac {\partial ln\mathrm {Z} }{\partial N}}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Se utilizarmos ${\displaystyle \Delta N=1}$ na aproximação, encontraremos a distribuição de Fermi-Dirac^[5]:

${\displaystyle <n_{s}>={\frac {1}{e^{\alpha +\beta \epsilon _{s}}+1}}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Ainda, o parâmetro ${\displaystyle \alpha }$ pode ser determinado pela primeira condição feita nesta dedução, em que

${\displaystyle \sum _{r}<n_{r}>=N}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

ou

${\displaystyle \sum _{r}{\frac {1}{e^{\alpha +\beta \epsilon _{r}}+1}}=N}$

Da relação entre a função partição ${\displaystyle Z}$ e a energia livre de Helmholtz ${\displaystyle F}$, sabemos que ${\displaystyle F=-k_{B}Tln\mathrm {Z} }$, logo:

${\displaystyle \alpha =-{\frac {1}{k_{B}T}}{\frac {\partial F}{\partial N}}=-{\frac {\mu }{kT}}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

${\displaystyle \alpha =-\beta \mu }$

onde ${\displaystyle \mu }$ é o potencial químico. Então outra forma de se definir a distribuição de Fermi-Dirac é^[5]:

${\displaystyle <n_{s}>={\frac {1}{e^{\beta (\epsilon _{s}-\mu )}+1}}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Quando os níveis de energia são muito próximos, de modo que podemos considerar que formam um contínuo, o número médio de partículas com energia entre ${\displaystyle \epsilon }$ e ${\displaystyle \epsilon +d\epsilon }$, pode ser escrito como^[5]

${\displaystyle n(\epsilon )=g(\epsilon )F(\epsilon )d\epsilon }$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Onde ${\displaystyle g(\epsilon )}$ é a densidade de estados, de modo que ${\displaystyle g(\epsilon )d\epsilon }$ fornece o número de estados com energia entre ${\displaystyle \epsilon }$ e ${\displaystyle \epsilon +d\epsilon }$. E ${\displaystyle F(\epsilon )}$ é a chama função de Fermi, dada por^[5]

${\displaystyle F(\epsilon )={\frac {1}{e^{(\epsilon -\mu )/k_{B}T}+1}}}$ / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Em mecânica estatística, a estatística Maxwell–Boltzmann descreve a distribuição estatística de partículas materiais em vários estados de energia em equilíbrio térmico, quando a temperatura é alta o suficiente e a densidade é baixa suficiente para tornar os efeitos quânticos negligenciáveis. A estatística Maxwell–Boltzmann é consequentemente aplicável a quase qualquer fenômeno terrestre para os quais a temperatura está acima de poucas dezenas de kelvins.^[1][2]

O número esperado de partículas com energia ${\displaystyle \epsilon _{i}}$ para a estatística de Maxwell–Boltzmann é ${\displaystyle N_{i}}$ onde:

${\displaystyle {\frac {N_{i}}{N}}={\frac {g_{i}}{e^{(\epsilon _{i}-\mu )/kT}}}={\frac {g_{i}e^{-\epsilon _{i}/kT}}{Z}}}$ 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

onde:

• ${\displaystyle N_{i}}$ é o número de partículas no estado i
• ${\displaystyle \epsilon _{i}}$ é a energia do estado i-ésimo
• ${\displaystyle g_{i}}$ é a degenerescência do nível de energia i, o número de estados dos partículas (excluindo o estado de "partícula livre") com energia ${\displaystyle \epsilon _{i}}$
• ${\displaystyle \mu }$ é o potencial químico
• ${\displaystyle k}$ é a constante de Boltzmann
• ${\displaystyle T}$ é a temperatura absoluta
• ${\displaystyle N}$ é o número total de partículas

${\displaystyle N=\sum _{i}N_{i}\,}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

• ${\displaystyle Z}$ é a função partição

${\displaystyle Z=\sum _{i}g_{i}e^{-\epsilon _{i}/kT}}$ / 

/ Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

• ${\displaystyle e^{(...)}}$ é a função exponencial, sendo e o número de Euler

A distribuição de Maxwell-Boltzmann tem sido aplicada especialmente à teoria cinética dos gases, e outros sistemas físicos, além de em econofísica para predizer a distribuição da renda. Na realidade a distribuição de Maxwell-Boltzmann é aplicável a qualquer sistema formado por N "partículas" ou "indivíduos" que interacambiam estacionariamente entre si uma certa magnitude ${\displaystyle m}$ e cada um deles têm uma quantidade ${\displaystyle m_{i}}$ da magnitude ${\displaystyle m}$ e ao longo do tempo ocorre que ${\displaystyle \sum _{i=1}^{N}M=m_{1}+m_{2}+...+m_{N}}$. / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Lei de Stefan ou Lei de Stefan-Boltzmann

Nos seus estudos da radiação de corpo negro Joseph Stefan chegou a seguinte função:^[8]

${\displaystyle R=P/A=\sigma T^{4}}$ / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Onde:

${\displaystyle A}$ = Área de emissão do corpo negro;

${\displaystyle R}$ = Potência irradiada por unidade de área (W/m²);

${\displaystyle P}$ = Potência total irradiada (W);

${\displaystyle \sigma }$ = 5,6705x10^-8W/m².K⁴ — também chamada de constante de Stefan;

${\displaystyle T}$ = Temperatura (K).

Esta expressão mostra que a potência irradiada por unidade de área varia apenas com a temperatura, ela não depende do material de sua cor entre outras características do corpo. O valor de R também indica a rapidez com a qual o corpo emite energia, por exemplo se a temperatura for triplicada a energia emitida será aumentada (3⁴=81) vezes ou se for quadruplicada a nova emissão será aumentada (4⁴=256) vezes. Corpos reais irradiam menos energia por unidade de área que o corpo negro, para calcular a energia irradiada por esses corpos é necessária a inclusão de um parâmetro denominado emissividade ε, a emissividade depende das características do material (cor, composição de sua superfície), seu valor fica entre zero e um.

Lei de deslocamento de Wien

O gráfico mostra o deslocamento dos picos de emissão do corpo negro; o produto da temperatura pelo comprimento de onda máximo se mantém constante com valor 2,898 x 10^-3 m.K

A emissão de radiação do corpo negro apresenta uma distribuição espectral que depende apenas da temperatura ${\displaystyle T}$. Seja ${\displaystyle R\left(\lambda \right)d\left(\lambda \right)}$ a potência emitida por unidade de área compreendida entre ${\displaystyle \lambda \ e\ \lambda +d\lambda }$. A figura 2 mostra valores da distribuição espectral ${\displaystyle R\left(\lambda \right)}$ em função de ${\displaystyle \lambda _{m}}$ para muitos valores de ${\displaystyle T}$ entre 3 500 K e 5 500 K.

Foi Wien quem pela primeira vez observou que o comprimento de onda máximo emitido era inversamente proporcional a temperatura do corpo negro e escreveu a equação que recebeu seu nome.^[8]

${\displaystyle \lambda _{m}\cdot T=constante=2,898\cdot 10^{-3}m\cdot K}$. / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Onde

${\displaystyle \lambda _{m}}$ = Comprimento de onda para o qual a emissão por unidade de área é máxima (m).

${\displaystyle T\ }$ = Temperatura do corpo negro (K).

Teoria de Planck da radiação de corpo negro

Ao tentar solucionar a discrepância entre a teoria e a experiência, Planck foi levado a considerar a hipótese de uma violação da lei da equipartição da energia sobre o qual a teoria se baseava. Planck supôs que a energia poderia ter apenas certos valores discretos, em vez de qualquer valor, e que os valores discretos fossem uniformemente distribuídos. Isto é, tomou

${\displaystyle E=0,\Delta E,2\Delta E,3\Delta E,4\Delta E,...}$ / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

como o conjunto de valores possíveis da energia. Aqui ${\displaystyle \Delta E}$ é o intervalo constante entre valores possíveis sucessivos da energia. Planck supôs também que as energias sucessivas e a frequência da radiação emitida fossem grandezas proporcionais, portanto,

${\displaystyle \Delta E\propto \nu }$ / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Escrito na forma de uma equação em vez de uma proporcionalidade, temos

${\displaystyle \Delta E=h\nu }$ / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

onde ${\displaystyle h}$ é a constante de proporcionalidade.

Cálculos posteriores permitiram a Planck determinar o valor da constante ${\displaystyle h}$, obtendo o valor que ajustava melhor sua teoria aos dados experimentais. O valor obtido por ele estava bem próximo do valor atualmente aceito

${\displaystyle h=6,63.10^{-34}J.s}$ / / Eψ ω Mom=   [/ ] /  / G ψ  = E ψ  = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

Esta constante, muito famosa e corrente na mecânica quântica, é chamada constante de Planck.

A fórmula obtida o permitiu calcular o espectro de corpo negro em total acordo com os resultados experimentais.

Postulado de Planck

A contribuição de Planck pode ser colocada na forma do seguinte postulado:

Qualquer ente físico com um grau de liberdade cuja "coordenada" é uma função senoidal do tempo (isto é, executa oscilações harmônicas simples) pode possuir apenas energias totais que satisfaçam a relação ${\displaystyle E=nh\nu }$ onde ${\displaystyle \nu }$ é a frequência da oscilação, ${\displaystyle h}$ uma constante universal e ${\displaystyle n}$ só pode assumir valores inteiros.

A energia do ente que obedece ao postulado de Planck é dita quantizada, os estados de energia possíveis são ditos estados quantizados, e o ${\displaystyle n}$ é dito número quântico.^[9]

Implicações

A ideia de que a energia é quantizada apesar de parecer apenas um truque matemático para explicar os resultados experimentais da radiação de corpo negro, foi fundamental para o desenvolvimento de um dos pilares da física moderna, a mecânica quântica.^[10]

Diagrama de Hertzsprung-Russell. As estrelas são classificadas por cor e luminosidade.

Exemplos de emissão de corpo negro

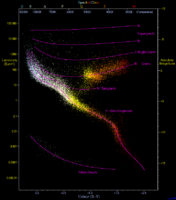
As diferentes cores das estrelas são um bom exemplo de corpos com espectros semelhantes ao de um corpo negro. As estrelas mais avermelhadas, como Antares e Betelgeuse, classificadas como tipo M no Diagrama de Hertzsprung-Russell, têm as menores temperaturas superficiais, enquanto as estrelas mais azuladas, como Rigel e Sirius, com classificação O ou B no diagrama H-R, têm temperaturas superficiais bem maiores.

Os materiais que, quando aquecidos, tornam-se incandescentes, também são bons exemplos de como a temperatura de um corpo interfere na sua emissão. Filamentos de lâmpadas incandescentes e uma barra de ferro aquecida são objetos presentes no cotidiano que emitem radiação com espectro próximo ao de um corpo negro.